进制转换方法(详细介绍)
计算机存储单位:
1、位,bit,是描述电脑数据量的最小单位,8bit=1字节;
2、字节,Byte,一个英文字母=8Byte,一个汉字=16Byte,1024个字节=1KB;
3、千字节,KB,1024KB=1MB;
4、兆字节,MBq,1024MB=1GB;
5、吉字节,GB,1024GB=1TB;
6、太字节,TB,1024TB=1PB;
7、拍字节,PB,1024PB=1EB;
8、艾字节,EB,1024EB=1ZB;1ZB相当于全世界海滩上沙子数量总和;
9、泽字节,ZB,1024ZB=1YB;
内存中以二进制形式存储数据,
二进制:0 1 逢二进一
0+0=0
0+1=1
1+1=10
10+1=11
11+1=100
100+1=101
101+1=110
110+1=111
111+1=1000
1000+1=1001
1001+1=1010
...
下面两张示意图详细演示了二进制加减法的运算过程。
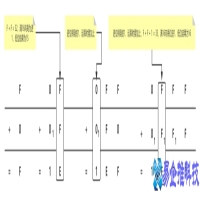
1) 二进制加法:1+0=1、1+1=10、11+10=101、111+111=1110

图1:二进制加法示意图
2) 二进制减法:1-0=1、10-1=1、101-11=10、1100-111=101

二进制减法示意图
八进制:0 1 2 3 4 5 6 7 ,逢八进一
下面两张图详细演示了八进制加减法的运算过程。
1) 八进制加法:3+4=7、5+6=13、75+42=137、2427+567=3216

图3:八进制加法示意图
2) 八进制减法:6-4=2、52-27=23、307-141=146、7430-1451=5757

八进制减法示意图
十六进制:0 1 2 3 4 5 6 7 8 9 a b c d e f ,逢16进一
注意,十六进制中的字母不区分大小写,ABCDEF 也可以写作 abcdef。
下面两张图详细演示了十六进制加减法的运算过程。
1) 十六进制加法:6+7=D、18+BA=D2、595+792=D27、2F87+F8A=3F11

图5:十六进制加法示意图
2) 十六进制减法:D-3=A、52-2F=23、E07-141=CC6、7CA0-1CB1=5FEF

十六进制减法示意图
十进制转“N”进制:倒除法,余数逆序.
1) 整数部分
将 N 作为除数,用十进制整数除以 N,可以得到一个商和余数;
保留余数,用商继续除以 N,又得到一个新的商和余数;
仍然保留余数,用商继续除以 N,还会得到一个新的商和余数;
……
如此反复进行,每次都保留余数,用商接着除以 N,直到商为 0 时为止。
把先得到的余数作为 N 进制数的低位数字,后得到的余数作为 N 进制数的高位数字,依次排列起来,就得到了 N 进制数字。
十进制数字 42 转换成二进制的过程:

从图中得知,十进制数字 42 转换成二进制的结果为 101010
下图演示了将十进制数字 36926 转换成八进制的过程:

十进制数字 36926 转换成八进制的结果为 110076
2) 小数部分
十进制小数转换成 N 进制小数采用“乘 N 取整,顺序排列”法。具体做法是:
用 N 乘以十进制小数,可以得到一个积,这个积包含了整数部分和小数部分;
将积的整数部分取出,再用 N 乘以余下的小数部分,又得到一个新的积;
再将积的整数部分取出,继续用 N 乘以余下的小数部分;
……
如此反复进行,每次都取出整数部分,用 N 接着乘以小数部分,直到积中的小数部分为 0,或者达到所要求的精度为止。
把取出的整数部分按顺序排列起来,先取出的整数作为 N 进制小数的高位数字,后取出的整数作为低位数字,这样就得到了 N 进制小数。
十进制小数 0.6875 转换成二进制小数的过程:

从图中得知,十进制小数 0.6875 转换成二进制小数的结果为 0.1011
十进制小数 0.930908203125 转换成八进制小数的过程:

十进制小数 0.930908203125 转换成八进制小数的结果为 0.7345
十进制整数与二进制、八进制、十六进制的对应关系:

注意,十进制小数转换成其他进制小数时,结果有可能是一个无限位的小数。请看下面的例子:
十进制 0.51 对应的二进制为 0.100000101000111101011100001010001111010111...,是一个循环小数;
十进制 0.72 对应的二进制为 0.1011100001010001111010111000010100011110...,是一个循环小数;
十进制 0.625 对应的二进制为 0.101,是一个有限小数。
本文地址:百科问答频道 https://www.neebe.cn/wenda/886544.html,易企推百科一个免费的知识分享平台,本站部分文章来网络分享,本着互联网分享的精神,如有涉及到您的权益,请联系我们删除,谢谢!



 相关阅读
相关阅读